Special Behaviors in morphoCA-(6,6,6)
Loops, Attractors, Topographies
Dr. phil Rudolf Kaehr
copyright © ThinkArt Lab Glasgow
ISSN 2041-4358
( work in progress, vs. 0.2, June 2016 )
Conceptual background
Claviatures gives a glimpse into the usefulness of the sub-rule approach for all kind of cellular automata. The merits of the sub-rule approach becomes evident for highly complex automata where it is practically not achievable to manipulate all single rules of the automaton explicitly.
With the sub-rule approach the single rule configuration that are defining an actual machine are constructed by the chosen keys of the claviature. Like for musical keyboards the melodies are composed by the chose of the keys and are not looked up from a look-up table of stored melodies.
The last presentation has shown a family of just 3 generations of the evolution of the complexity of morphic cellular automata realized in the modi of graphics, structure and sound. Here, a next step in the evolution is presented.
The evolution is: from ![]() to
to ![]() and to
and to ![]() , now extended to
, now extended to ![]() of
of ![]() .
.
A DCKV rule of morpho![]() , like {3,0,1,3,4}→2, has a morphic rule complexity r of 6 ( {3,0,1,3,4,2}), a word length n of 5 ({3,0,1,3,4}), a value complexion k of 6, (1,2,3,4,5,6) and a succession s width of 1 ({x}→2).
, like {3,0,1,3,4}→2, has a morphic rule complexity r of 6 ( {3,0,1,3,4,2}), a word length n of 5 ({3,0,1,3,4}), a value complexion k of 6, (1,2,3,4,5,6) and a succession s width of 1 ({x}→2).
The concept of claviatures for generalized morphic cellular automata is presented at:
http://demonstrations.wolfram.com/ClaviaturesForGeneralizedCellularAutomata/
And obviously at my website: http://memristics.com
Special features of ![]()
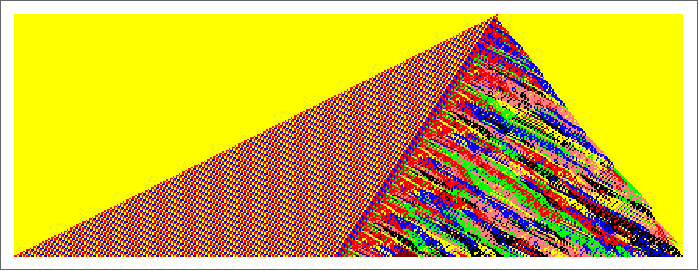
Some experimentations with the automata of ![]() demonstrates quickly surprising features and behaviors unknown to the previous developments of morphogram-based automata.
demonstrates quickly surprising features and behaviors unknown to the previous developments of morphogram-based automata.
A first surprising pattern arised as a closed behavior of a form similar to a ‘pinched hysteresis’ loop. The next figure that crossed my attention was a stable figure on a double background. Other stable patterns are easily found with the help of the claviature for ![]() . Certainly, there are millions of more familiar patterns. Many of them are a kind of a differentiation of previous patterns.
. Certainly, there are millions of more familiar patterns. Many of them are a kind of a differentiation of previous patterns.
A collection of patterns will be added to: http://www.yumpu.com/en/rkaehr
Structured Loops
Loops, attractors or Eigen-Forms are a well known topic in the theory of dynamic systems. In the field of cellular automata they appear prominently in 2-dimensional CAs.
In this paper, transformations are mapped on 1-dimensional topologies.
It seems that there are no structured loops in classical 1-D CAs. They also don’t appear in morphogrammatic CAs of complexity 3- to 5, i.e. ![]() to
to ![]() .
.
Questions of shortes and longest morphoCA loops are not yet tackled in this paper.
Topics of self-referentiality in morphoCAs are accessible by:
http://memristors.memristics.com/MorphoSR/MorphoSub.html
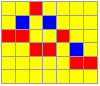
An elementary loop is given by the following example. It is embedded in anenvironment and has 2 distinctive elements. The cycle has a ‘handle’ of two elements that might be activated in the context of chains of structured loops. The loop closes with just 4 steps. All further steps are enlarging the environment of the closed figure.
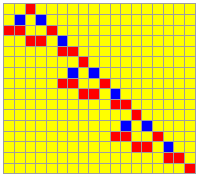
Chains of structured Loops
The example shows the elementary mechanism of chaining structured loops. The loops are alternating and augmenting their complexity from 2 to 3 elements in an endles chain. There are also strictly iterative connections of a loop.
Iterative chaining
Alternating and augmenting chaining
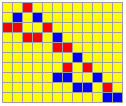
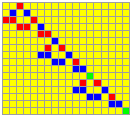
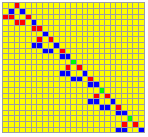
A slightly more complex elementary chain of structured loops is given by the iterating and complexity augmenting chain of double loops.
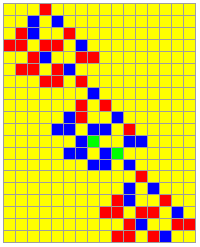
Chains of structured loops are not always obvious.


Closed Formations

This automaton produces a closed form after 14 steps embedded in a double evolving environment.
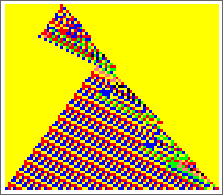
Systems of overlapping triangles

Open borders

Topographies

Hats
Overlappings


The graph shows clearly two centres of two overlapping patterns.
Complementarities


The patterns is composed by two complementary order systems: a regular and a non-regular.
What are the order-theoretic features of morpho![]() ?
?
It seems that the classical categories or paradigms of order have to be redefined by an extension to new, untill now unknown concepts.
A very first simple scheme might be written as:
Order from order.
Order from disorder.
Order from (Order and disorder). These are the 3 von Foerster/Gunther order principle. A new might occurr as:
Order from (neither order nor disorder).
Attractors in 1 D CAs?
https://theory.org/complexity/cdpt/html/node4.html
http://www.informatik.uni-giessen.de/automata2013/talk-22.pdf
Random based pattern

Requisites
DCKV-(6,6)-11,12
Procedure666
DCKV-(6,6)-123
DCKV-(666)-5
Claviature for morphoCA-(6,6,6)
Special patterns out of morphoCA-(6,6,6)’s poly-verse
Structured Loops

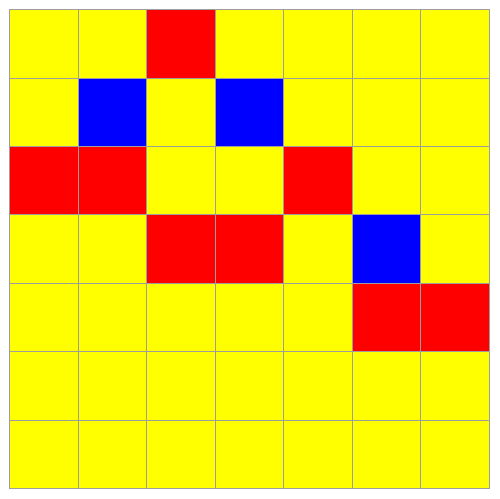
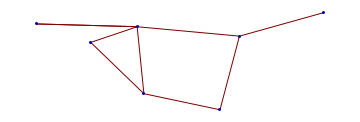
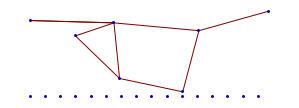


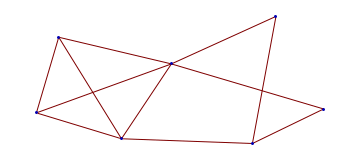
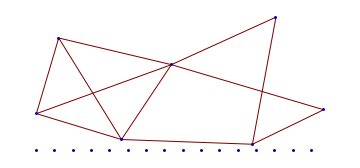
![]()


Chains of Loops




![]()


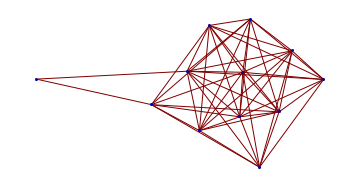





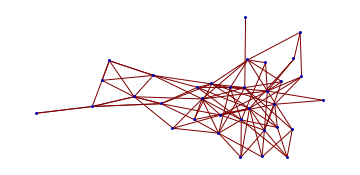






![]()






![]()






![]()





Closed Forms

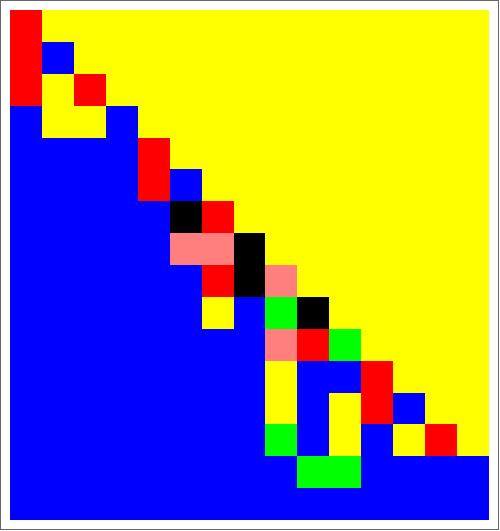



![]()


![]()

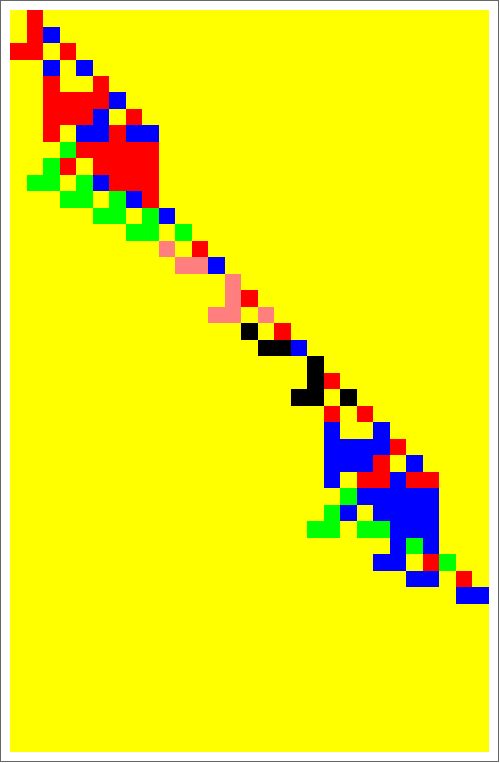
Systems of triangles
![]()







Open borders


Topographies

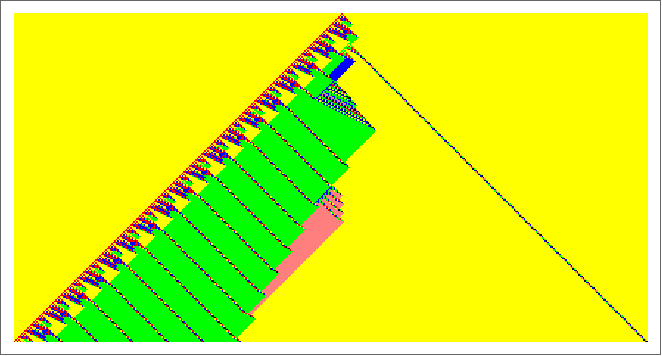



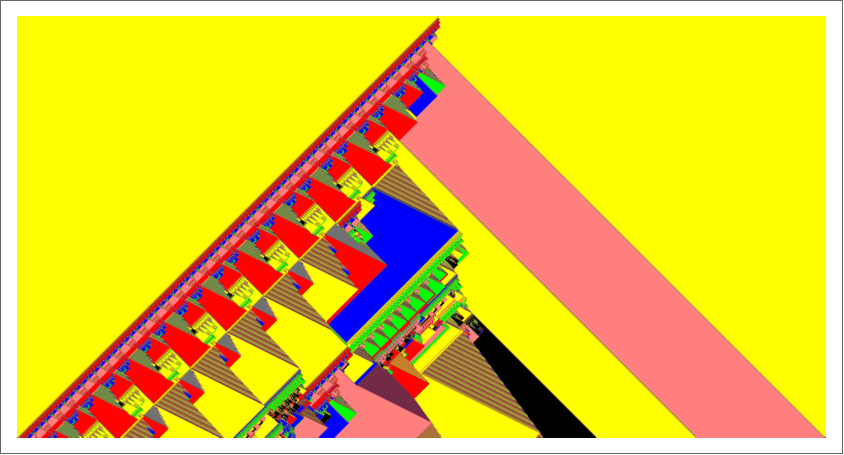




Hats

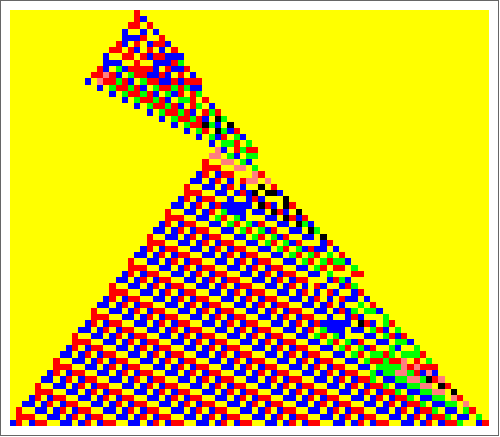
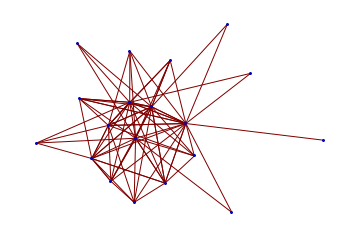

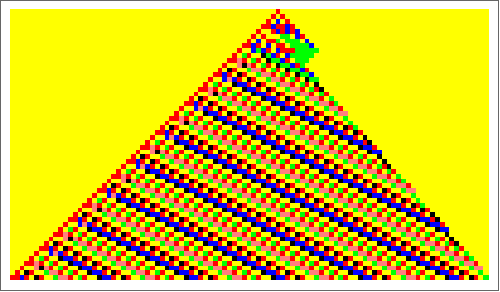
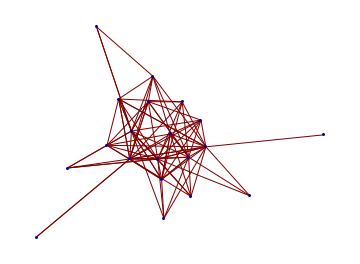
Overlappings







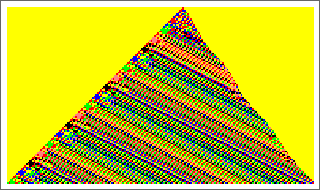
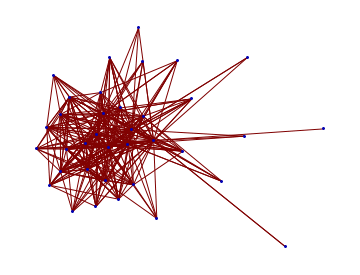
Complementarities