Aristotelian and NON-Aristotelian LOGIC

by GOTTHARD GÜNTHER 

What kind of thought process should be expected
of the seetee alien mind?

- part 2 of 4 -

It is pretty well established that the human mind can think only in Aristotelian categories. Mechanical brains, however, will work differently and will eventually be able to "think" in non-Aristotelian forms of reasoning. 

There is one specific kind of mechanical brain which will not work at all unless it is equipped with the machinery of non-Aristotelian thinking. That is the thought translator. Well and good! But what is a non-Aristotelian thought process? Obviously, to answer this question we must first examine the classic logic of Aristotle. The discovery of formal logic is a very recent affair in the history of mankind. It hardly dates more than twenty-five hundred years back. 

The first discovery of formal logic in Ancient Greece - the so-called Sophists -were rather like traveling magicians or first-rate circus performers of our days. You paid your admission and watched the "artist" perform his tricks. He would, for instance, single out a man from the audience and address him as follows, "You admit, sir, that you have that which you have not lost?"

The innocent answer was, "Of course."

"Then, my friend," the Sophist blandly continued, "as you never lost a tail, you must have a tail."

The performer might select a woman known to be a shrew and ask her, "Madam, have you stopped beating your husband? Answer ´yes´ or ´no!´ " This proved an embarrassing alternative.

Among those laughing at the befuddled woman was a man with a dog. The Sophist turned to him and inquired, "Is this your dog?"

"Yes."

"I see it is a female dog. Has she had puppies?"

The proud owner of the dog affirmed it.

Diabolically the Sophist concluded, "This dog has two properties. First, it is your dog, and second it is mother. Let's add up the predicates: this dog is your mother." 

The performer's mental gymnastics were successful because it was little known in pre-Aristotelian times that formal logic is based on a strict technique, and that the skillful "logician" can do amazing tricks when using (or misusing) that technique. Audiences today more sophisticated and not so easily fooled. 

Now, if logic is a rational technique it can be technically handled. This is done by the method of propositional calculus Propositional calculus is the technique of combining logical statements according to their truth values. In order to, symbolize any two statements, we use the letters p and q /1/. We also use the tilde (~ ) which is supposed to represent the negation, and a dot (· ) which shall have the meaning AND. We therefore read ~p as NONp, and p· q as pANDq. The letters p and q may represent any two statements we choose. However, to work with our symbols, ~ and · , we have first to fix their meaning and show how they work. This is done for the negation by the following table:

This table indicates that if p is true, then ~ p is false, and if p is false, then ~ p must be true. Instead of the letter T for true and F for false, we have inserted the first two natural numbers for greater convenience. We will later develop tables for a non-Aristotelian logic, and this can be done more easily by dealing with numbers than with letters. 

It is this table which has given Aristotelian logic the name of a two-valued logic. Any statement in this technique of thinking must have one of the two values: it is either true (1) or false (2). No third value exists. True (1) and false (2) are mutually exclusive. The other term · (AND) is similarly defined. AND is supposed to convey a connection between two statements. When we say "the sun shines AND the wind blows", the two independent statements about the sun and wind are merged into a compound-statement by connecting them through the word AND. The problem now is to find out under which logical condition the compound statement shall be true. It stands to reason that the truth of the two independent statements is a question of meteorology rather than of logic. We shall, therefore, give them all possible truth-values. We shall call the statement about the sun p and that about the wind q. We then find that the following combinations are possible:

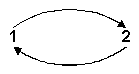
The first line under the horizontal bar tells us that both statements are true. According to the second line it is true that the sun shines. But there is no wind. The statement q is false. From the third line we derive that p is false. There is no sunshine; but the second statement is true. The wind does blow. The last line finally informs us that there is neither sun nor wind. Both statements, p as well as q are false. It is evident that the two columns give all possible truth combinations for the two independent statements. But now let us melt these two single statements into a compound statement, "the sun shines AND the wind blows". That raises the question: in which of the above-described cases will the compound statement also be true? We write our compound statement in symbolic form, p· q, and now design a more comprehensive table which contains besides the single statements p and q also the compound elements, p· q:

It is obvious that the compound statement, "the sun shines and the wind blows" can be true in one and only one case, namely if the sun as well as the wind are active. If there is no wind, then p· q is false. If there is no sun and only wind it is also false. The same applies if there is neither sun nor wind - in other words if p as well as q both have the value 2. The expression p· q is only true if p as well as q are separately true.

By means of this table a logically exact definition of the logical meaning of AND has been obtained. This meaning is used by the electrical calculators if they "think" a conjunction. By the way, the same can be done for the meaning of "OR" in the inclusive or exclusive sense for "IMPLY", for "IS EQUIVALENT TO ", for "IS COMPATIBLE WITH", and for "NEITHER-NOR". There is no need for us to develop the truth tables of all these logical connectives. They can be derived from a combination of and p· q. The table of negation and the table "AND" together represent the whole propositional truth-structure of Aristotelian logic. They are therefore sufficient basis to develop from there the entire propositional truth-structure of a non-Aristotelian logic. 

Our terran mentality is Aristotelian. There is no doubt about that. But sometimes we meet in life non-Aristotelian situations where our two-valued thinking fails to give us a proper answer. This story, told by an Indian logician, describes such a non-Aristotelian situation.

A Maharajah who kept a large game preserve for his private amusement was constantly troubled by poachers. Losing his patience, he proclaimed that every poacher caught by his guards would suffer capital punishment. Moreover, to add spice to his pronunciamento, the prince decreed that every delinquent facing execution should be privileged to make a statement. If this statement were shown to be true, the condemned man was entitled to beheading; if it proved to be false he should be burned alive. Presently the Maharajah's game warden caught a man shooting deer. On the day of execution the poacher was reminded of his privilege to make a statement. Cleverly he worded it as follows: "I shall be burned alive."

This perplexed the judiciary committee which was to rule on the truth of his statement. The judges were faced with an unavoidable dilemma: if we burn the poacher, then his statement turns out to have been true and he is entitled to a beheading. However, if we chop off his head his statement proves to be false and he should have been burned. At latest reports the committee was still deliberating.

The difference between the Sophistic trick-question and the Indian paradox lies in the fact that the former questions result from the misapplication of the formal rules of Aristotelian logic. It is very easy to rectify them. The dilemma of the condemned poacher on the other hand is not solvable within the confines of the classic logic of Aristotle. Moreover, it suggests a problem that has recurred within the modern mathematical theory of transfinite sets. So far there exists no genuine solution for it. Only some makeshift procedures have been just instituted by dint of which it is possible to circumvent the awkward dilemma (e.g. Bertrand Russell's theory of types). So far only one thing can be said with certainty. All attempts to solve this and other logical paradoxes point in a direction which leads us away from the Aristotelian mode of thinking towards a new system of trans-classical, non-Aristotelian logic. Let's pursue the train of reasoning which the Indian paradox offers us. 

All Aristotelian logic is characterized by a very strict limitation. It cannot make any valid statements except about past events. Aristotle's system is, as we have demonstrated, a two-valued order of thought. Any statement subject to it is either true or false and must be judged as such. It stands to reason that the strict alternative of the two statements:

"This event did take place"

or (exelusive)

"This event did not take place"

is only applicable to the past. As far as the future is concerned, this strictly dichotomic occurrence pattern does not apply. A proposition about the future has only probability value. Its final and absolute truth-value remains in abeyance as long as the future remains the future. It should be added that the more a future event approaches the present, the more the probability range narrows down - but probably it remains till it passed the critical mark of the present. From then on only it can be said that it has taken place ¼ or not.

Now let us apply these reflections to the statement of the condemned poacher. He has stated, "I shall be burned alive". There, is no way of verifying this proposition and establishing this truth-value before the execution has taken place. But the execution cannot take place before the statement has been verified, since the mode of the execution depends the truth or falsity of the poacher's statement. The vicious circle is perfect.

There is indeed no genuine solution of the paradox on the basis of two value- thought processes. But let us take another look at this baffling problem. In view of this dilemma, the judges might decide that the Maharajah's stipulation does not apply to this case and consequently accord this prisoner an entire different treatment. That might be anything from hanging to dismissal of the case and the prisoner's release. As long as the future is concerned, there now exists three distinct probabilities: burning, 2) beheading, 3) something else. It follows the strict alternative to the two-valued logic of "to be or not be" does not adequately cover the pattern of future events. Therefore we need at least a three-valued logic, and any statement about the future should be phrased according to the laws of such a non-Aristotelian system of logic thought. 

It should be understood that a genuine third value must represent a total rejection of the alternative represented by the other two values. In Aristotelian logic the two values true (1) and false (2) mutually, reject each other individually. Therefore, prisoner and judges alike are caught in the vicious circle.

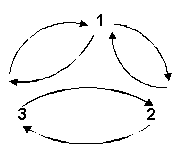
In a three-valued logic there exists an additional rejectional relation apart from the mutual rejection of any two values. The following diagram might help. We add to our classic value a third value.  

As this value rejects the preceding alternative of true and false, and so to speak displaces them, we shall call it the displacement value and designate it with the number 3. But what does this number mean? Don't try to understand it! I the professional logician do not know either. We don't have to. As we will later see that becomes the function of the mechanical brain. The following triangular pattern of the values is only meant to show you the increasing complexity of a three-valued relationship of logical concepts.

We then discover an interesting sequence of values. First 1 ("I shall be burned") is rejected and we proceed to 2. Then 2 is rejected also. In a two-valued logic this would inevitably lead us back to 1 and we would have entered the vicious circle. But now the situation is different. Apart from the mutual negation (rejection) of 1 and 2 there now exists an analogue relation between 2 and the new value, 3. That means there is a logical choice for our argument. It can either return from 2 to 1, thus completing the two-valued paradox, or it can also proceed from 2 to 3. In fact, this latter course is exactly what will happen. It will happen for the following reason: 1 has already been rejected, and 3 has not, so far as our paradox is concerned. In other words, 3 now occupies a position of logical preference. 

But what does 3 really mean in terms of our Indian paradox? According to our convention, 1 indicates the burning, 2 stands for decapitation. In order to find out about 3, let us take another look at the diagram. If we do so we shall discover that 3 does not only reject 2, it also rejects 1 and is in turn rejected (negated) by both classical values. This produces an entirely new rejectional relation. 3 not only rejects 1 and 2 individually, it rejects, moreover, the whole alternative which is represented by the mutual opposition of 1 and 2. To put it differently: 3 not only rejects the contrasting features of 1 and 2, it also negates that which the first two values have in common. Burning and beheading indicate different choices of capital punishment. And, since 3 rejects the alternative of 1 and 2, it negates not only the individual instances of burning and beheading but it rejects their common denominator capita1 punishment. 

It is logically impossible, therefore, that 3 might mean hanging. This is implied by the first and most basic law of any three-valued logic. First find out what the common denominator of the first two values is - in other words the general basis upon which they negate each other - and then deny this very basis. But you might well ask: is it always possible to determine the common denominator?' You are quite right, that is where the difficulty comes in and why a three-valued logic is a matter for somebody else, but not for us.

There must be some reason why we humans use the Aristotelian logic although it has a very limited scope and cannot deal with certain problems.

Let us go back once more to our Indian paradox and try to find out why this is so. We noted that the common denominator for burning and beheading was supposed to be capital punishment. But why not just punishment? It should do as well. In this case the third value would represent non-punishment and the prisoner might expect a complete pardon. But why not generalize even more and simply say: some action by the committee. This might lead to a bonus for the poacher or even a reward for having pointed out an essential flaw in the directive of the Maharajah. In fact, there is no limit to this trend of generalization. We might as well go to the limit and say that the common denominator of burning and beheading is that both are events in the world. However, as the 3 value negates the common denominator we should arrive at the idea of "no event" as last solution. But where does that leave the judge or the prisoner? Neither of them could ever go home because that too would be an event. 

This clearly shows that there is no point to us in adopting a three-valued logic because it works only if the scope of the alternatives that are used in its system are, arbitrarily limited. On the other hand a logic misses its purpose altogether if it does not permit us to produce statements of any degree of general validity. There is one alternative of absolute generality the human mind is capable of. It is contained in Shakespeare's famous line: "To be, or not to be that is the question." 

Undoubtedly that line contains the most radical two-valued alternative that could be thought. of. Let us try to add to the positive value of "being" and the negative value of "not being" a third non-Aristotelian value. We know the procedure now. First we have to find the common basis for "being" and "not being" and then reject the same. The ensuing result should provide us with the meaning of the third value. But what is the common denominator of "being" and "not-being", i.e. - of "something" and "nothing"? There obviously is no common basis. You may rack your brain till doomsday. You will never find a mysterious essence that "being"' and "not being"' have in common. They are total negations with no common, bond.

"To be, or not to be-" that is the final question that takes precedence over everything. The comprehensive scope and the generality of Shakespeare's. alternative can never be surpassed. There is, therefore, no third value on that level. The two-valued, Aristotelian logic reveals itself as the most general form of thinking of which the mind is capable. 

In my. first article "The Seetee Mind" I have demonstrated that man is incapable of thinking except with an Aristotelian logic due to the peculiar energetic (electric) qualities of physical existence. The present article shows that there are also purely logical reasons which confine terrestrial intelligence to the two-valued pattern of rational thought. Yet we have seen that even in human existence there are certain situations and aspects which are not covered by the Aristotelian mode of thought. The Indian paradox demanded a three-valued, non-Aristotelian technique of thinking. It is evident that such a technique exists, but we were not able to fit it systematically into our habits of reasoning. 

The possibility of many-valued, non-Aristotelian systems of logic is to date a scientifically established fact because the various calculi which would correspond to the mental activities of a non-Aristotelian intelligence have already been worked out. Still the spiritual (rational) life of Man does not conform to non-Aristotelian, patterns. This too can be accepted as an established fact. Obviously somewhere something is missing in our present conception of the relation between man and cosmos. 

The mystery deepens if we reflect upon the possible opposition of an Aristotelian and a contra-Aristotelian mind. My preceding article developed the thesis that a seetee mind would represent a total negation of our own. Let us try to follow that argument a bit further. Shakespeare gave us the formula for the total opposition of the two values. It is the disjunction of "to be" or "not to be". If that is so, then all our rational concepts define "being". Reversely, all concepts in a contra-Aristotelian mind should designate "not being." Even more: the seetee mind is for us "not being!" All right, if something does not exist why should we go to any trouble about it. I am afraid we must, because there's an awkward twist to the matter. What we have just described is the onesided terrene viewpoint. Seen from the contraterrene angle the shoe is entirely on die other foot. For the seetee mind only contraterrene mentality represents "being" and Aristotelian thought pattern is the dear index of non-existence. 

The relation is mutual: the Aristotelian and contra-Aristotelian mind simply do not exist for each other. But somehow they must co-exist - if contra-terrene matter is a physical reality. The reason is obvious: a mind may ignore the existence of another mind, but terrene matter cannot ignore the physical reality of contraterrene matter if both happen to collide in space. Then the whole show goes off with a bang. You certainly cannot expect more positive recognition of one's own total negation.

Therefore, if seetee matter exists, then the reality of the contraterrene mind is also implied. We shall probably never contact a seetee mind physically because between its realm and ours yawns an existential void where only mutual self-annihilation of physical matter governs the rules of a possible encounter. But there exists a ´Third´ in this creation beside Matter and the energetic Mind: it is Information.

Information can bridge the cosmic gulf. This, however, demands the design of a brain that stands halfway between the terrene and the contraterrene intelligence. Only a robot brain could do that. An artificial brain with a non-Aristotelian thought pattern. A brain of that type is theoretically possible. My next article will explain how.

Footnotes:

/1/ In the interest of readability we have varied from the standard punctuation of symbolic logic and omitted quotation marks from the symbols preferring the use of capital letters (AND, OR, etc.).

/2/ The double line means that the 3rd column is a result of the first two columns

vordenker Contact: webmaster@vordenker.de
Copyright © Gotthard Günther 1959
Issued: September 2, 1997
Last modified (layout) 2010-12-06