|
|
life as polycontexturalitysome remarks on part_1by Eberhard von Goldammer As it was pointed out in the Günther 2000 special a contexture is a logical domain where all classical logical rules hold strictly. Furthermore we pointed out that Günther uses the term many-valued logic in a different way. In Günther´s terminology many-valuedness has to be interpreted in the sense of a many-placed logical system, i.e., there are different logical places (locations) that are characterized by different contextures. As logical domains, these contextures are not isolated from each other but rather mediated by new logical operators such as global negations and/or the transjunction. In other words:
If a contexture is considered to be isolated, i.e., intra- or monocontextural, it is basically classic. On the other side, if a contexture will be considered in relation to other contextures, i.e. inter- or polycontextural, it is discontextural. Discontexturality means that there is no continuity, no medium, no space, no language, etc., in common with other contextures. However, as it was already mentioned, contextures are not isolated logical domains but rather mediated by inter- or transcontextural logical operations (!!).
The number of contextures nK depends on m the number of logical places or positions that characterize a logical discourse and it also depends on the valuedness s within the sub-systems, the single contextures. With m £ s the number of contextures is:
which is
For three logical positions (m = 3) and an
intracontextural valuedness of two (s = 2), it follows:
and correspondingly for m = 4 and s = 2, the number of contextures is nK = 6 At a first glance, one would expect a similarity between a polycontextural system (with m = 3 and s = 2) and Peirce´s triadic logic. However, any similarity turns out to be more or less superficial with both classical (monocontextural) or non-classical (polycontextural) interpretations:
0 . . . . . . . . . . . . . ½ . . . . . . . . . . . . . 1
0 . . . . . . ¼ . . . . . . ½ . . . . . . ¾ . . . . . . 1 etc. ...
Within these short remarks we cannot discuss in detail any possible apparent relationships between Peirce´s triadic logic and PCL. Instead we will shortly point at some fundamental differences.
While the PCL is a calculus, these triads have to be interpreted with the help of an adequate calculus. This is the most significant and obvious difference between the triads and Günther´s PCL. In "Cybernetic Ontology and Transjunctional Operations" Günther has shown that any triadicity without an adequate concept of distribution between the different (logical) positions is simply reduced to a single logical domain, i.e., to one contexture and therefore all these triadic models remain basically dichotomic (cf. part_4 of Günther_2000special). In other words, neither von Foerster´s concept of eigen-values nor Spencer Brown´s calculus of indication (CI) or Varela´s variation of an extended_CI represents an adequate basis for a consistent formal model of Peirce´s and/or any other triadic relationships. Although the smallest polycontextural unit is given by three contextures (m=3), one can easily show that polycontexturality begins with four (m = 4) and not with three (the triad, m = 3) which means that a complete logical system only results with m = 4 and not with m = 3. It is needless to say that m < 3 is meaningless. In other words, the smallest meaningful polycontextural logical system is given by a structure with four (logical) positions distributed/mediated over six two-valued logical domains/contextures (or four three-valued contextures, or one four-valued contexture). Within these short introducing remarks on polycontexturality we would like to point out that not only the "law of excluded middle" – the tertium non datur – has two different meanings, but also the concept of identity. The classical concept of identity strictly holds intracontextural, i.e., within a contexture. A non-classical concept of identity becomes possible and it allows mutatis mutandis the modeling of an identity distributed over several contextures. A well-known example is the distribution of subjectivity over the categories of I, THOU, and IT which can only be modeled within a polycontextrual framework. If one considers the importance of the classical law of identity for mathematics, for example, for the development of numbers, it might not be such a surprise if we mention that PCL also represents a basis for the development of a mathematical concept of polycontextural or qualitative numbers, qN. However, this point will be discussed in a forthcoming contribution. Within the 1st of 3 parts in this series we present the following papers of Gotthard Günther:
|
|
|
vordenker Contact: webmaster@vordenker.de |
||


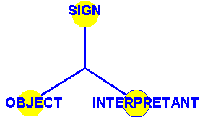 Peirce´s
triadic relation between sign, object, and interpretant represents neither a
logical system nor a calculus. Actually, this relation corresponds to von
Foerster´s model of cognition which can be summarized as follows:
"environment is the triadic relationship E(W,C,D) between the domains W
(real world), C (cognitive processes), and D (descriptions)."
Peirce´s
triadic relation between sign, object, and interpretant represents neither a
logical system nor a calculus. Actually, this relation corresponds to von
Foerster´s model of cognition which can be summarized as follows:
"environment is the triadic relationship E(W,C,D) between the domains W
(real world), C (cognitive processes), and D (descriptions)."